2차원 배열의 합은
https://www.acmicpc.net/problem/2167
백준 2167번 문제를 통해 접하게 되었음!!
처음에 이해하기가 너무 어려웠음!! 😂
2차원 배열의 합을 들었을 때는 배열 안에 있는 숫자만 다 더하면 되는 거 아닌가??🤔 라는 생각이 들었음!
백준문제를 풀 때도 쉽겠는데!!~라는 생각으로 접근했는데
그게 아니었음!!!!!
2차원 배열의 합을 구하기 위해서는 DP를 이용해야 함!
어떻게 구하는지 알아보자 ~~!!!
🎯 1차원 배열의 합
우선 1차원 배열의 합부터 알아보자
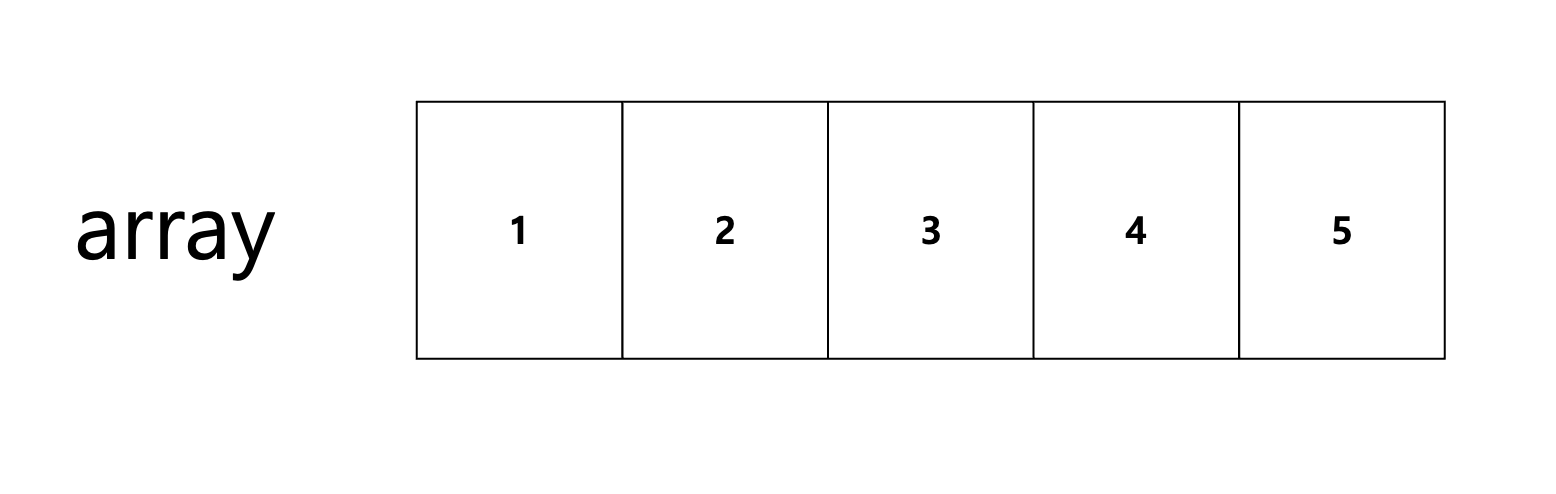
위와 같은 1차원 배열이 있을 때

배열의 합을 저장하는 dp의 모습임
0번 index에는 array[0]까지의 합
1번 index에는 array[0, 1]까지의 합
2번 index에는 array[0, 1, 2]까지의 합
3번 index에는 array[0, 1, 2, 3]까지의 합
4번 index에는 array[0, 1 , 2, 3, 4]까지의 합으로 만들어짐!
dp를 구하는 점화식은
dp[i] = dp[i-1] + array[i]
만약 i가 3이라서 dp[3]을 구한다고 가정해 보자

dp[3] = dp[2] + array[3]를 한 값이 됨
dp의 2번 index에는 array[0, 1, 2]까지의 합
dp의 3번 index에는 array[0, 1, 2, 3]까지의 합이기 때문임
swift 코드로 구현해 보면
let array:[Int] = [1, 2, 3, 4, 5]
var dp = arr
for i in 1..<array.count {
dp[i] = dp[i-1] + array[i]
}
// [1, 3, 6, 10, 15]
위와 같고 ~
let array:[Int] = [1, 2, 3, 4, 5]
var dp = Array(repeating: 1, count: 5)
for i in 1..<array.count {
dp[i] = dp[i-1] + array[i]
}
// [1, 3, 6, 10, 15]
이렇게도 가능함!!! 근데 dp 배열을 만들어줄 때 1로 넣어주어야 함!!
처음에 0으로 넣어서 만들었는데 i가 1일 때 dp[0] + array[1] = dp[1]이 2가 나오면서 틀린 답으로 나오게 됨!
🎯 i ~ j 까지 배열의 합
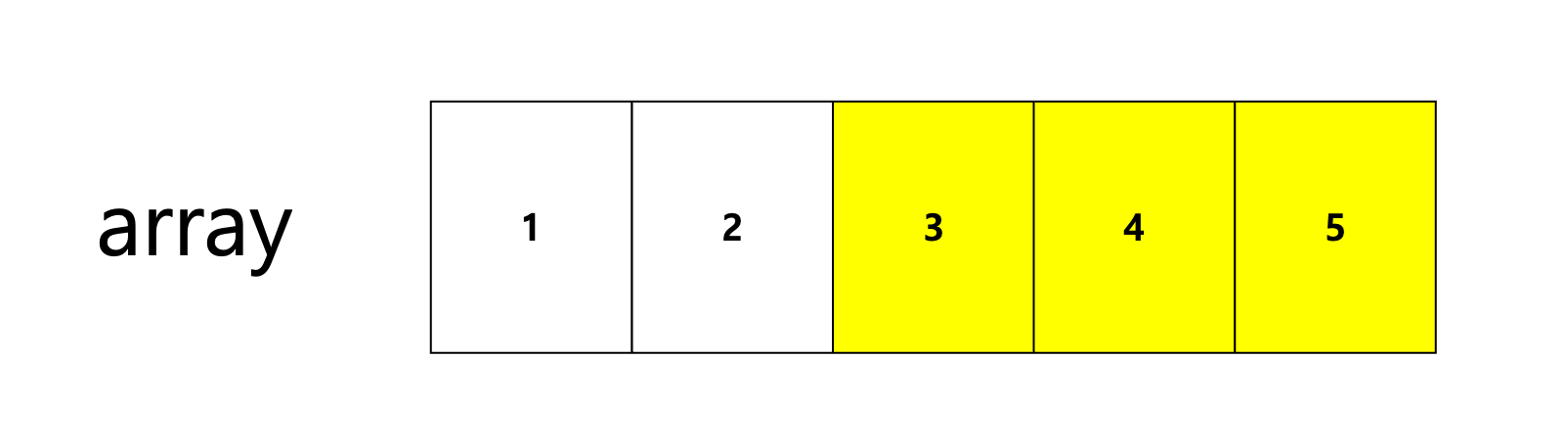
만약 array[2] ~ array[4]까지 요소의 합을 dp를 이용해서 구하고 싶다고 가정하자
dp[4]는 array[0~4]까지의 합인데,
구해야 하는 건 array[2~4]의 합임!!
즉 array[0~1]의 합, dp [1]의 값을 빼주면 됨!
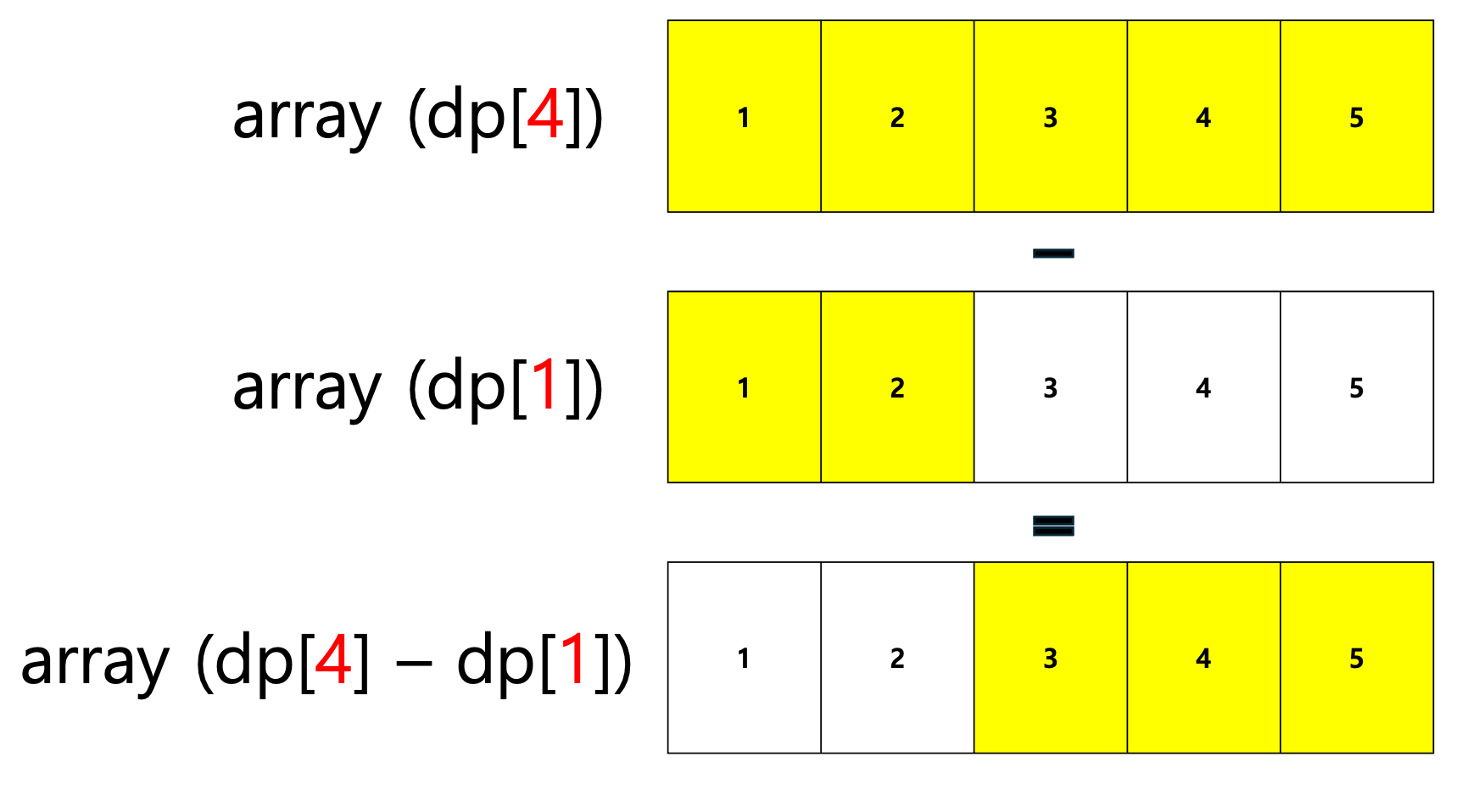
dp[4] - dp[1]을 해주면 array[2~4]까지의 합을 구할 수 있음.
i ~ j (i < j)까지 배열의 합에 대한 점화식은
array[i~j]까지의 합 = dp[j] - dp[i-1]
🎯 2차원 배열의 합
본격적으로 2차원의 배열을 알아보자!
2차원 배열에서의 합의 dp는
해당 index(dp[i][j])를 오른쪽 아래 끝점으로 하는 사각형 안에 있는 배열의 합이라고 함
1. dp[1][1]

(1, 1)을 오른쪽 아래 끝점으로 하는 2차원 배열의 사각형은 위와 같은데!
dp[1][1]은 array[0~1][0~1]까지의 값을 모두 더한 값 14가 되는 것임.
2. dp[2][3]

(2,3)을 오른쪽 아래 끝점으로 하는 2차원 배열의 사각형은 위와 같음
dp[2][3]는 array[0~2][0~3]까지의 값을 모두 더한 값 78이 됨~!!
사각형 안에 있는 배열의 합(dp [i][j])을 어떻게 구해지는를 보면!!

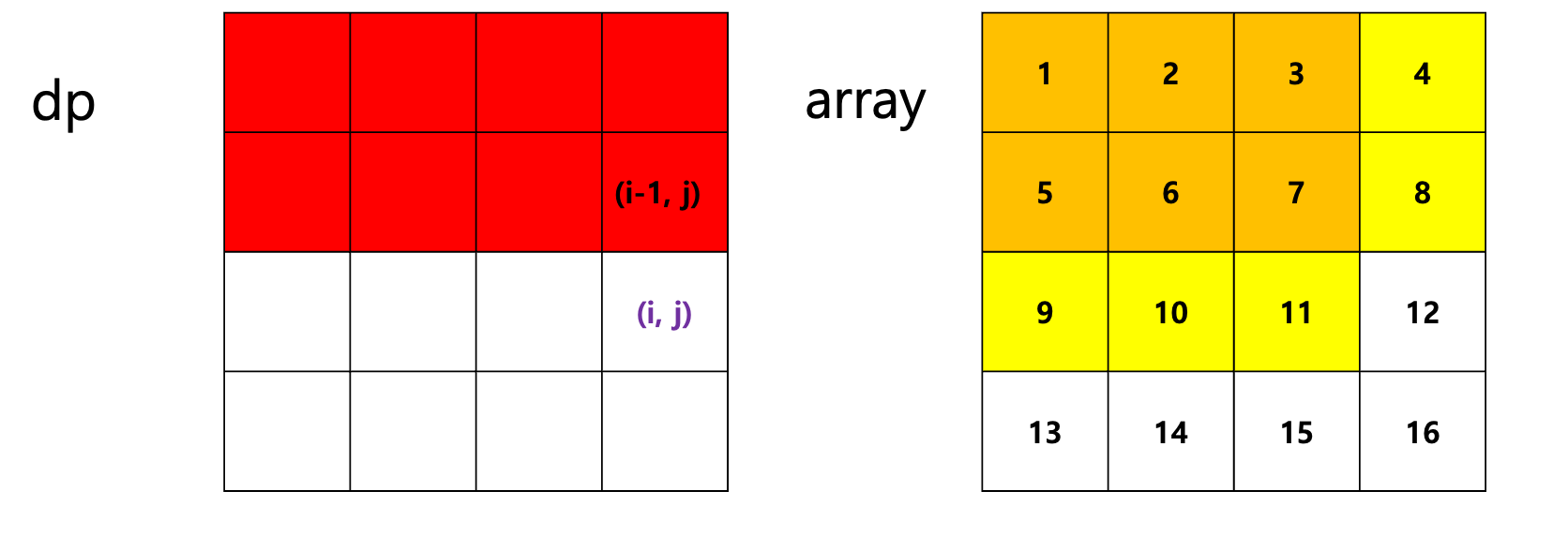
dp[i][j]를 구하기 위해서는
dp[i][j-1]의 값과 dp[i-1][j]의 값을 더해주는 것임
만약 i, j가 (2, 3)이라면, array로 봤을 때 1, 2, 3, 5, 6, 7이란 값이 중복으로 더해지고 있음 (주황 부분)

따라서 중복으로 더해진 dp[i-1][j-1]을 빼주어야 함!!
그리고 마지막으로
그리고 마지막으로
array[i][j] 값을 더해주면 dp[i][j] 값이 나오게 됨!!
따라서 이를 점화식으로 나타내면
dp[i][j] = dp[i-1][j] + dp[i][j-1] - dp[i-1][j-1] + array[i][j]
Swift 코드로 작성해 보면
import Foundation
let array:[[Int]] = [[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12], [13, 14, 15, 16]]
var dp = Array(repeating: Array(repeating: 0, count: 5), count: 5)
for i in 1...4 {
for j in 1...4 {
dp[i][j] = dp[i-1][j] + dp[i][j-1] - dp[i-1][j-1] + array[i-1][j-1]
}
}
for i in 1...4 {
print(dp[i][1...4])
}
// [1, 3, 6, 10]
// [6, 14, 24, 36]
// [15, 33, 54, 78]
// [28, 60, 96, 136]
이렇게 dp를 구할 수 있음
dp는 array보다 size를 각각 1씩 더 줘서 만듦.
때문에 array에 접근할 때 array[i-1][j-1]이 됨.
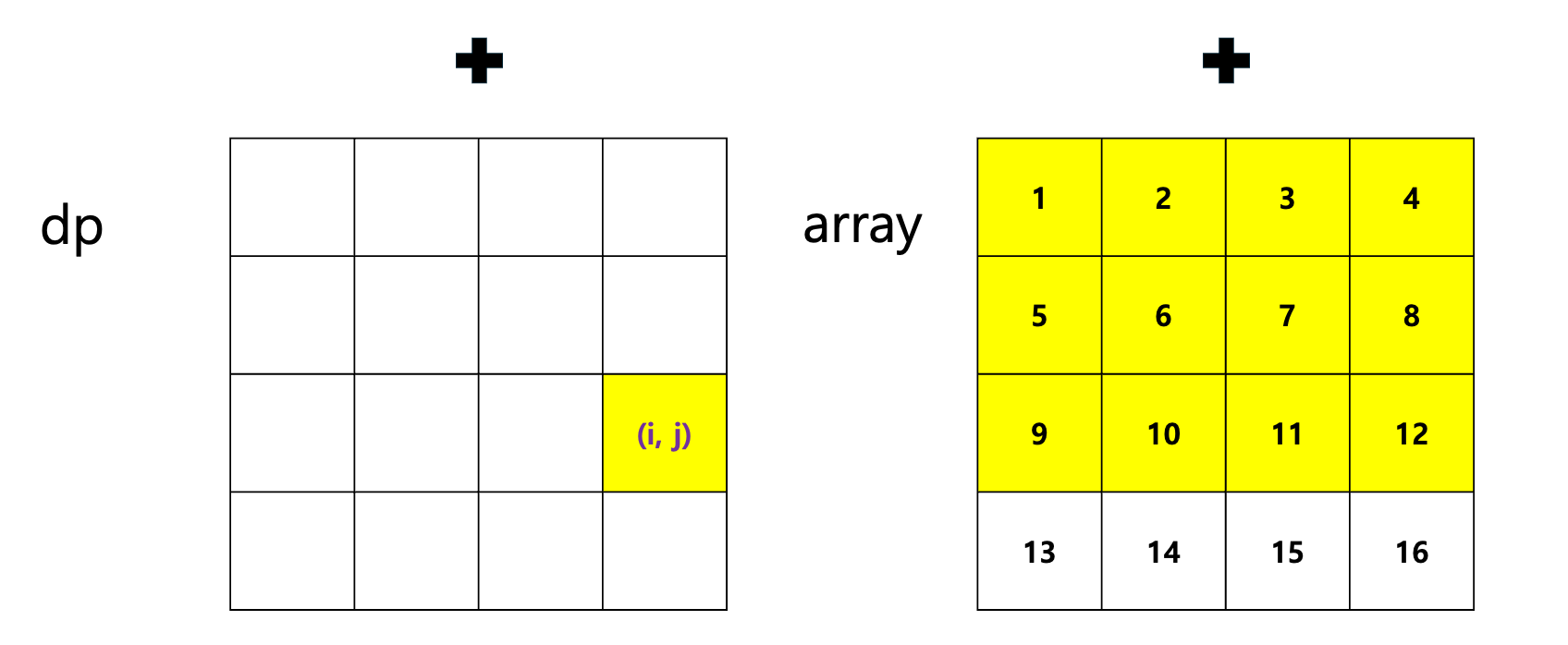
3. (i, j) ~ (x, y)까지 배열의 합
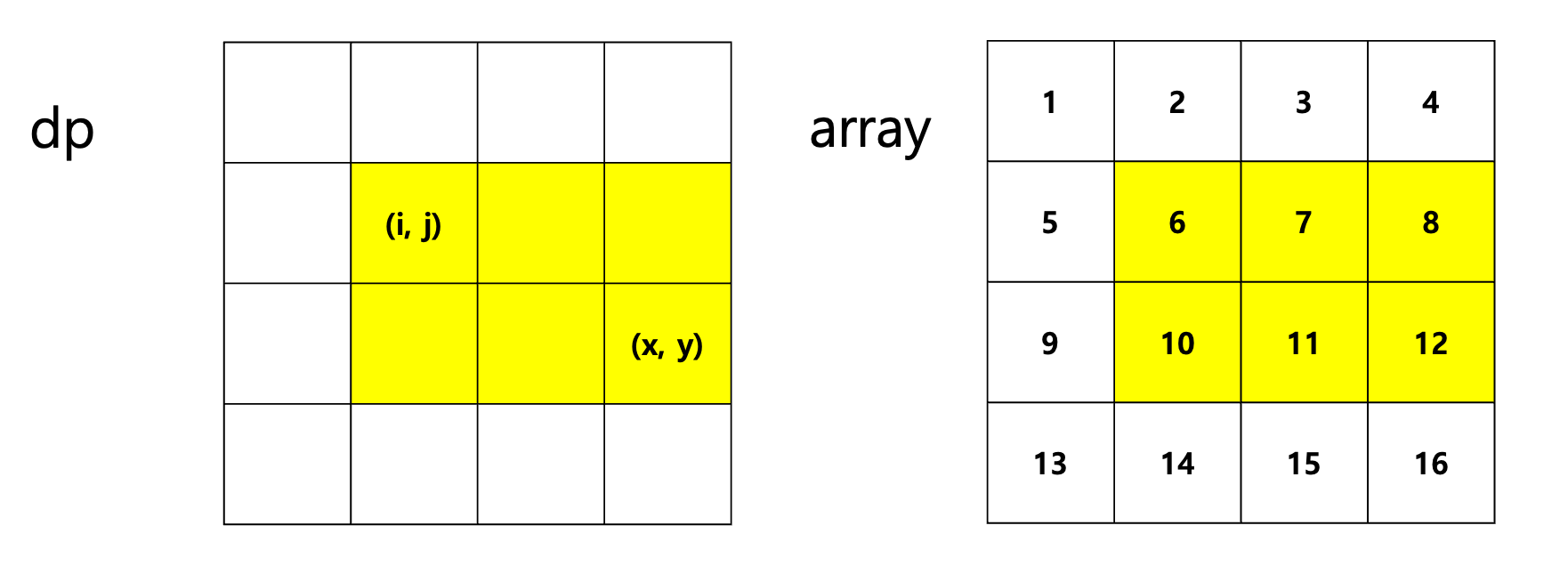
(i, j) ~ (x, y)까지 배열의 합을 어떻게 구하냐면!
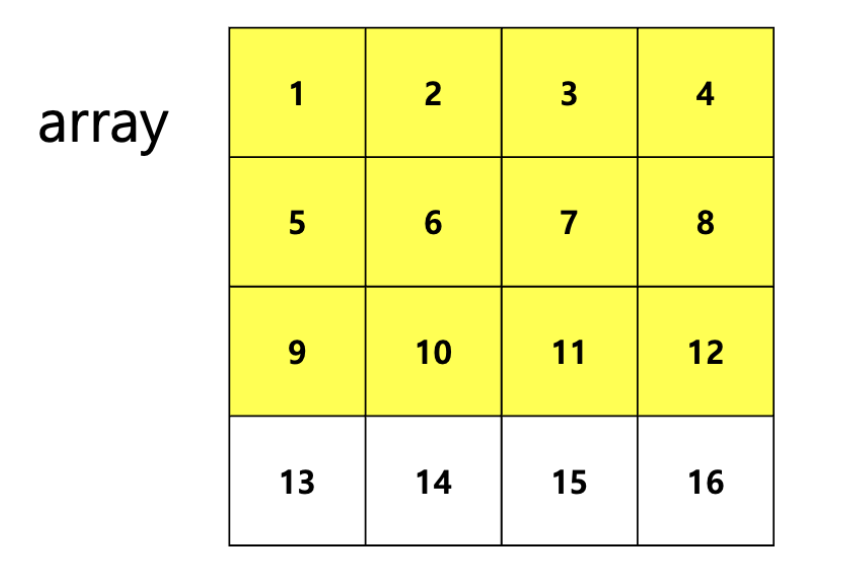
dp의 (x, y)는 위와 같이 노란색 영역이 모두 더해져 있음.
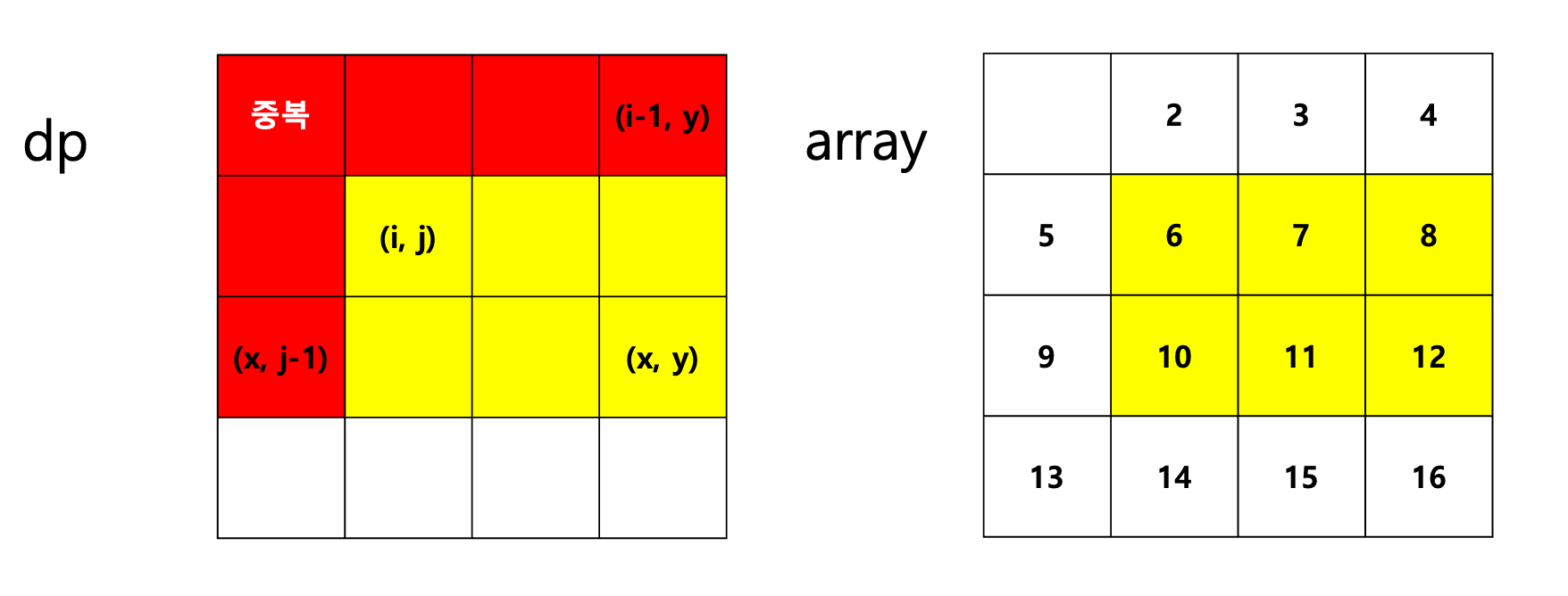
더하고 싶은 영역이 아닌 사각형 dp[x][j-1]와 dp[j-1][y]를 빼주어야 하는데
그런데 이때 중복되어서 빼지는 부분이 생기기 때문에!!
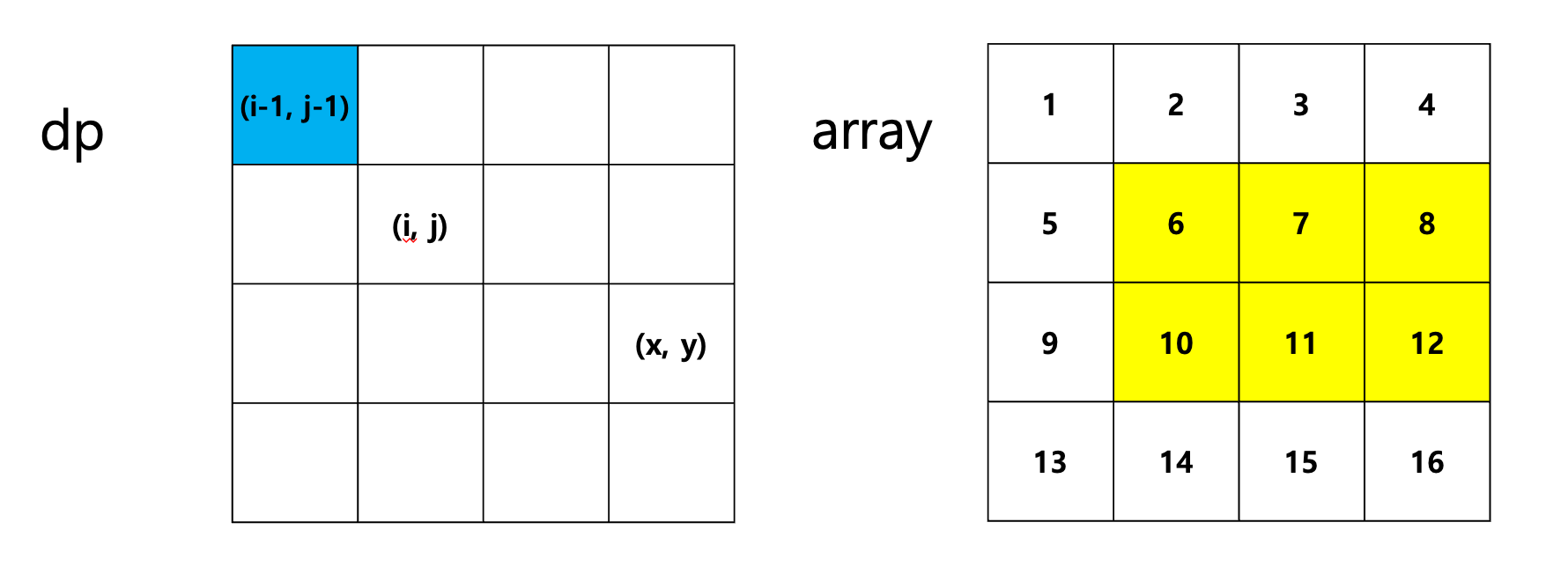
중복되어 빠져 버린 부분인 dp[i-1][j-1]를 더해주면 됨!
점화식으로 보면
array[i][j] ~ array[x][y]까지의 합 = dp[x][y] - dp[i-1][y] - dp[x][j-1] + dp[i-1][j-1]
Swift 코드로 작성해 본다면
(i, j)는 (1, 1)이고 (x, y)는 (2, 3)일때 (1, 1) ~ (2, 3)까지 배열의 합을 구해본다면
mport Foundation
let array:[[Int]] = [[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12], [13, 14, 15, 16]]
var dp = Array(repeating: Array(repeating: 0, count: 5), count: 5)
for i in 1...4 {
for j in 1...4 {
dp[i][j] = dp[i-1][j] + dp[i][j-1] - dp[i-1][j-1] + array[i-1][j-1]
}
}
for i in 0...4 {
print(dp[i][0...4])
}
// [0, 0, 0, 0, 0]
// [0, 1, 3, 6, 10]
// [0, 6, 14, 24, 36]
// [0, 15, 33, 54, 78]
// [0, 28, 60, 96, 136]
let (i, j, x, y) = (2, 2, 3, 4)
print(dp[x][y] - dp[x][j-1] - dp[i-1][y] + dp[i-1][j-1])
// 54
i, j, x, y의 값이 1씩 더해진 이유는 dp는 array보다 size를 각각 1씩 더 줘서 만들었기 때문임!
한번 정리해 보고 백준문제를 다시 풀어보면서 적용까지 해보았음!
이렇게 하지 않았으면 다시 이 문제를 접할 때 또 막막하기만 했을 거 같음!!
잘 정리해 본 만큼 가끔 다시 보면서 안 까먹도록 하겠음!!!!!
참고 및 인용
'Algorithm' 카테고리의 다른 글
| [Algorithm] Swift 백준 1244번 (2) | 2024.05.27 |
|---|---|
| [Algorithm] Swift 백준 2167번 (0) | 2024.05.24 |
| [Algorithm] Swift 백준 2563번 (3) | 2024.05.19 |
| [Algorithm] Swift 백준 1002번 (0) | 2024.05.06 |
| [Algorithm] Swift 백준 18110번 (1) | 2024.04.14 |



