https://www.acmicpc.net/problem/1002
문제접근

문제를 처음 볼 때 좌표라는 말에 너무 꽂혀서 좌표에 있는 점들을 기준으로만 생각함 r이 3이라면 (0,3), (3,0), (3, 3)만 생각한 거임.. 그러나 보니 어떻게 겹치는 점을 계산해야 할까??라는 생각에서 나아갈 수 없었음....
그래서 접근방법만 참고를 했음!!
문제는 원을 성질을 이용해서 풀어야 하는데 다시 생각해 보면 좌표 기준으로 r만큼 떨어져 있기 때문에
r만큼 떨어진 곳을 찍어보면 원의 둘레에 재명이가 위치하게 되는 거였음!!
정답풀이
우선 규현과 승환의 두 점 사이의 거리를 구함.

문제를 보면

하나의 점을 기준으로 거리 r만큼 떨어진 거리에 재명이가 있을 수 있는 좌표가 존재하게 됨.
그러면 두 좌표가 떨어져 있는 거리에 따라 재명이가 있을 수 있는 위치의 수가 달라질 것임!!
그래서 두 점 사이의 거리를 구하는 거임!!!!!
1번째

만약 두 명의 좌표가 같을 때는 재명이가 있을 수 있는 위치가 무한대가 됨!!
무한대일 때는 -1을 출력해 줌!!!
2번째

만약 두 점사이의 거리가 r1 + r2의 값보다 크면 재명이가 존재할 수가 없음!!
0을 출력해 줌!!
3번째

만약 내부에서 두 원이 만나지 않는 경우에는 재명이가 있을 수 있는 위치가 존재하지 않음
0을 출력해 줌!!
4번째
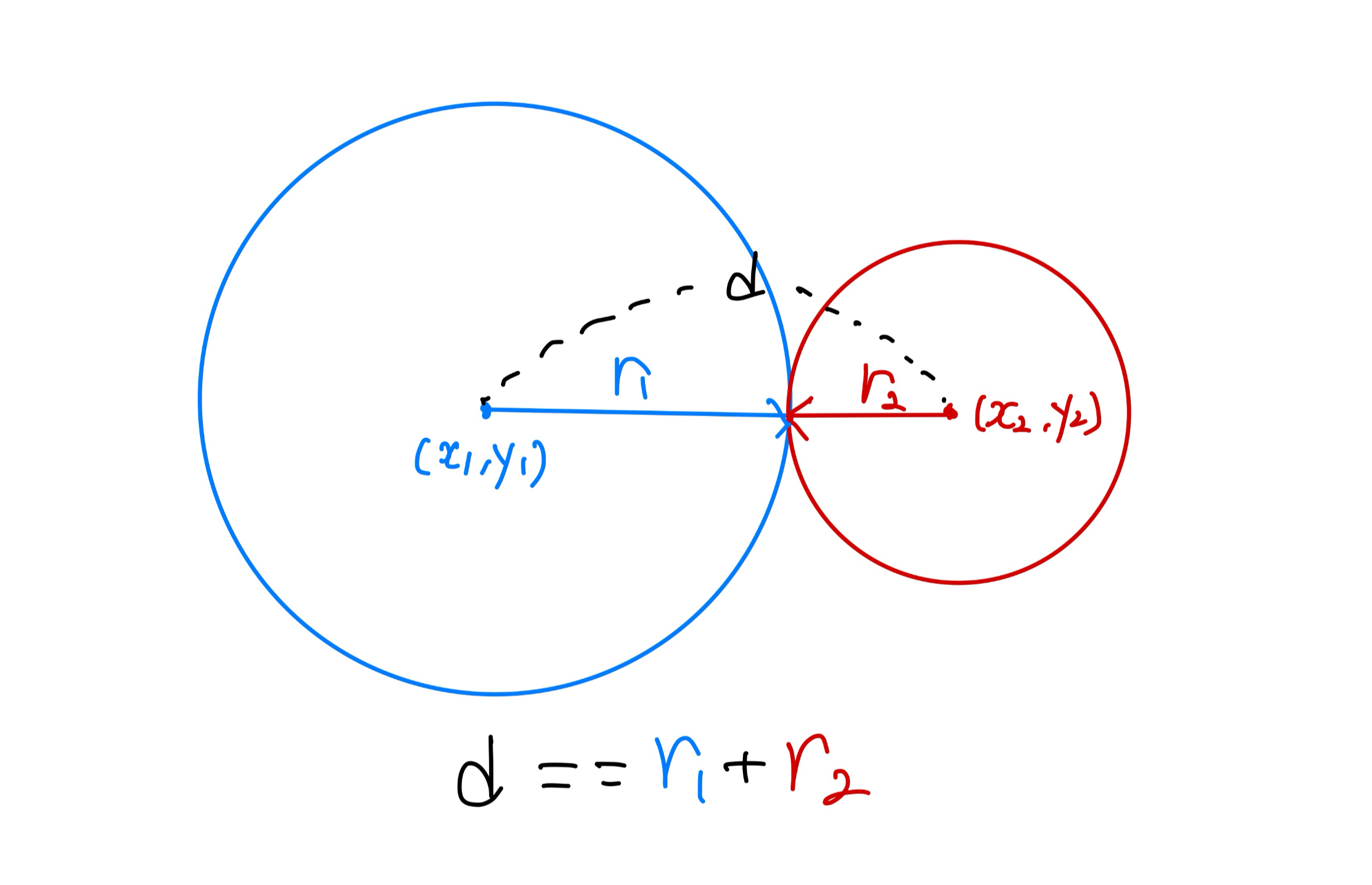
만약 두 점 사이의 거리가 r1 + r2와 같다면 두 개의 원은 한 점에서 만나게 되며, 재명이가 있을 수 있는 위치는 1개가 존재함
1을 출력해 줌!!
5번째
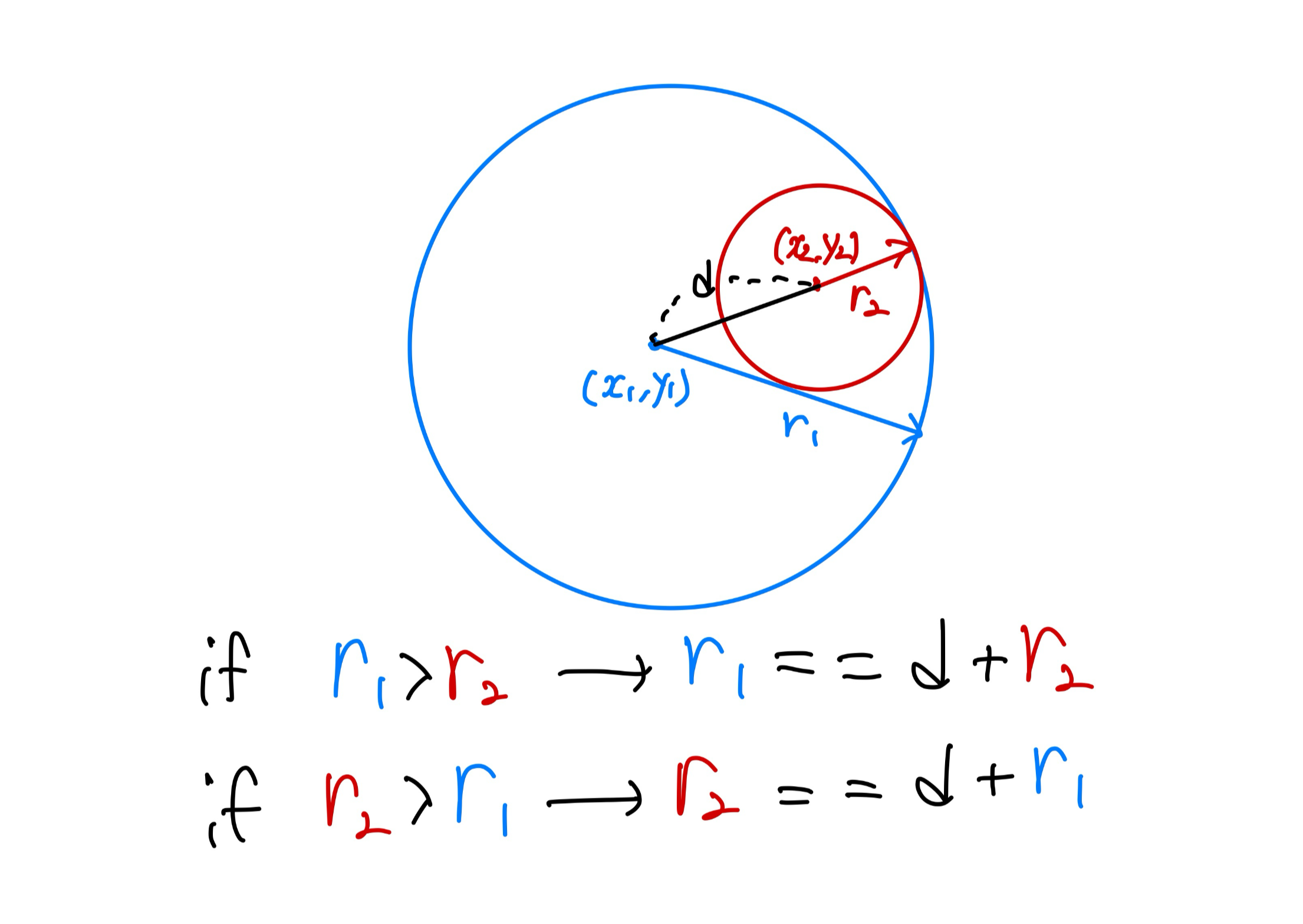
내부에서 두원이 만나는 경우도 한 점에서 만나게 되며, 재명이가 있을 수 있는 위치 1개가 존재함!
1을 출력해 줌!!
6번째

만약 두 원이 겹치면 만나는 점이 2개가 생김, 재명이가 있을 수 있는 위치가 2개가 존재
2를 출력해 줌!!
Swift 코드로 구현해 보면
import Foundation
// 테스트 케이스 주어짐
let T = Int(readLine()!)!
for _ in 0..<T {
let input = readLine()!.split(separator: " ").map { Double(String($0))! }
var (x1, y1, r1, x2, y2, r2) = (input[0], input[1], input[2], input[3], input[4], input[5])
// 두 좌표간 거리
var d = sqrt(pow((x1 - x2), 2) + pow((y1 - y2), 2))
// 같은 좌표일떄
if x1 == x2 && y1 == y2 && r1 == r2 {
print("-1")
} // 만나지 않는 경우
else if d > r1 + r2 || (r1 > r2 && d + r2 < r1) || (r2 > r1 && d + r1 < r2) {
print("0")
} // 한점에서 만나는 경우 (외부에서 힌 점에서 만나는 경우, 내부에서 한 점에서 만나는 경우)
else if d == r1 + r2 || (d + r1 == r2) || (d + r2 == r1) {
print("1")
} else {
print("2")
}
}
'Algorithm' 카테고리의 다른 글
| [Algorithm] Swift 1차원, 2차원 배열의 합 (1) | 2024.05.24 |
|---|---|
| [Algorithm] Swift 백준 2563번 (3) | 2024.05.19 |
| [Algorithm] Swift 백준 18110번 (1) | 2024.04.14 |
| [Algorithm] Swift 백준 15829번 (0) | 2024.04.13 |
| [Algorithm] Swift 백준 10773번 (3) | 2024.04.06 |



