최근 코테문제를 매일 풀면서 소수 찾기 문제를 풀게 되었음.
근데 항상 시간초과가 생기거나 어떻게 풀어야 할지 접근이 어려웠음!!
그때마다 항상 다른 분들이 에라토스테네스의 체로 소수문제를 해결했음!!
이번에 잘 공부해 두면 큰 도움이 될 거 같음!!
자! ~~ 한번 알아보자!!
우선 에라토스테네스의 체는 수학에서 소수를 찾는 쉽고 빠른 방법임!!
마치 체로 치듯이 수를 걸러낸다고 하여 '에라토스테네스의 체'라고 불린다고 함!!
코드를 보기 전에 어떻게 동작하는지 간단하게 보자!
- 2부터 소수를 구하고자 하는 구간의 모든 수를 나열한다. 그림에서 회색 사각형으로 두른 수들이 여기에 해당한다.
- 2는 소수이므로 오른쪽에 2를 쓴다. (빨간색)
- 자기 자신을 제외한 2의 배수를 모두 지운다.
- 남아있는 수 가운데 3은 소수이므로 오른쪽에 3을 쓴다. (초록색)
- 자기 자신을 제외한 3의 배수를 모두 지운다.
- 남아있는 수 가운데 5는 소수이므로 오른쪽에 5를 쓴다. (파란색)
- 자기 자신을 제외한 5의 배수를 모두 지운다.
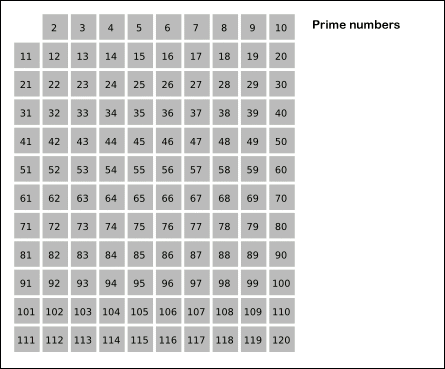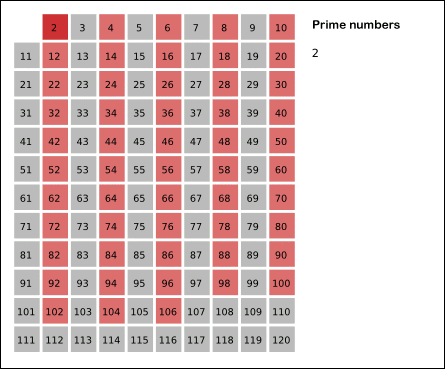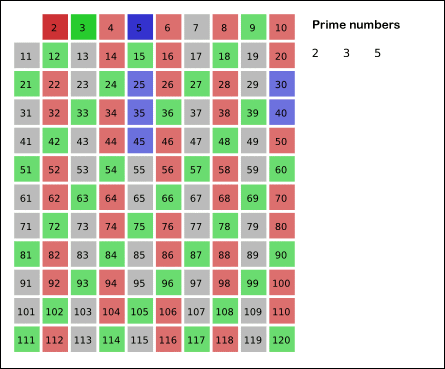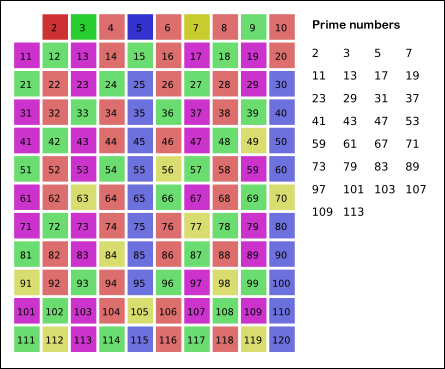
- 남아있는 수 가운데 7은 소수이므로 오른쪽에 7을 쓴다. (노란색)
- 자기 자신을 제외한 7의 배수를 모두 지운다.
- 위의 과정을 반복하면 구하는 구간의 모든 소수가 남는다. (보라색)
그림의 경우, 112>120
이므로 11보다 작은 수의 배수들만 지워도 충분하다. 즉, 120보다 작거나 같은 수 가운데 2, 3, 5, 7의 배수를 지우고 남는 수는 모두 소수이다.
푸는 방법이 다양하게 존재할 수 있지만 이분 🔽 코드가 잘 이해가 되어서 이걸 기준으로 작성하였음!!
https://dev-mandos.tistory.com/93
[알고리즘] 에라토스테네스의 체 (Swift)
에라토스테네스의 체 에라토스테네스의 체 알고리즘은 고대 그리스 수학자인 에라토스테네스가 만들어낸 소수를 찾는 알고리즘 입니다. 마치 체로 치듯이 수를 걸러낸다고 하여 '에라토스테네
dev-mandos.tistory.com
Swift 코드로 작성을 해보면!
우선 지금 소수를 찾는 범위가 1 ~ 100까지라고 정하자!!
var isPrimeNumber = [Bool](repeating: true, count: 101)
코드상으로는 101만큼의 크기인 Boolean Array를 true로 초기화를 해줌
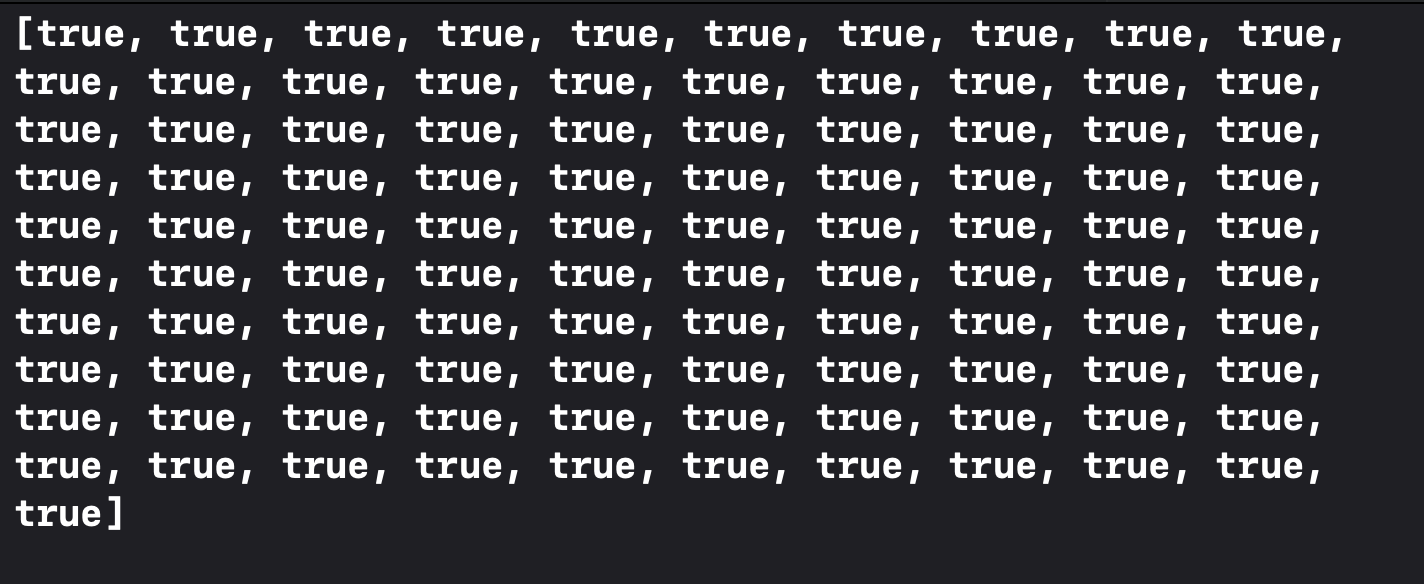
숫자 표로 보면 🔽

근데 여기서 생각이 든 게??? 🤔 1 ~ 100까지인데 왜?? 101개를 만들어줄까 의문이 들었음!!
일단 넘어가 보고.. 소수가 될 수 없는 1을 먼저 제거해 주자
isPrimeNumber[1] = false
요렇게 해주면
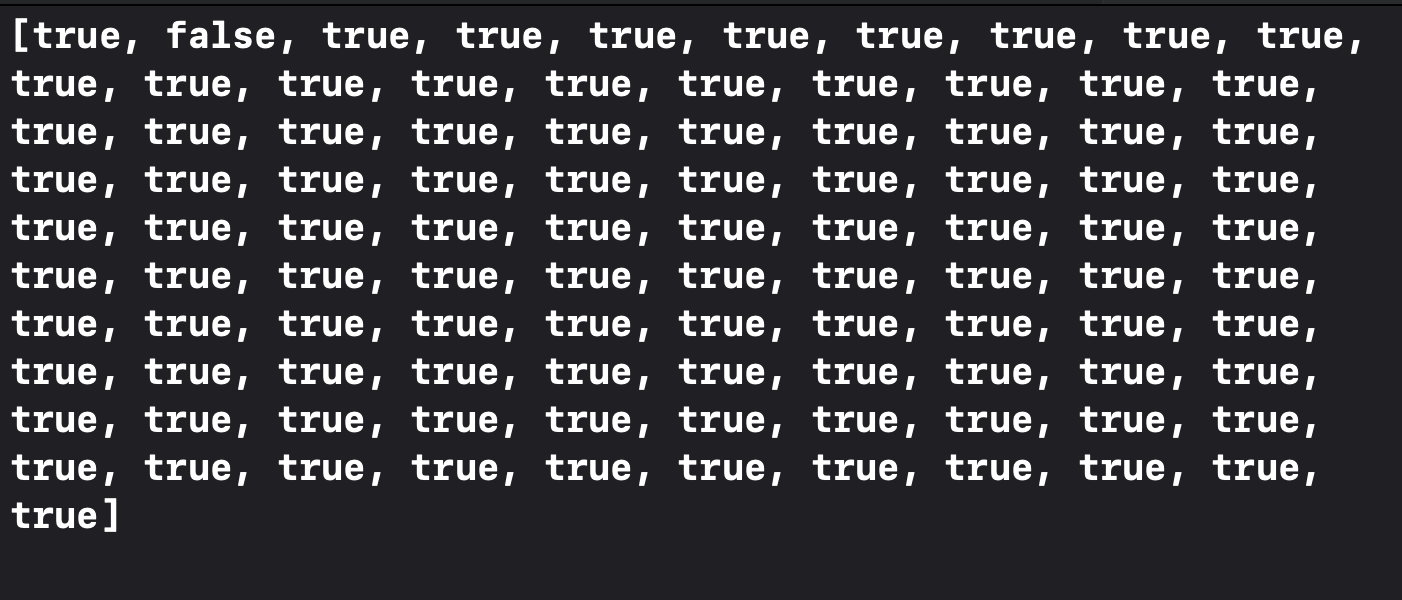
배열에 1번째 자리가 false로 바뀌게 되는데
그럼 다시 의문으로 돌아가서 이번에는 count를 100개로 만들어서 해보자
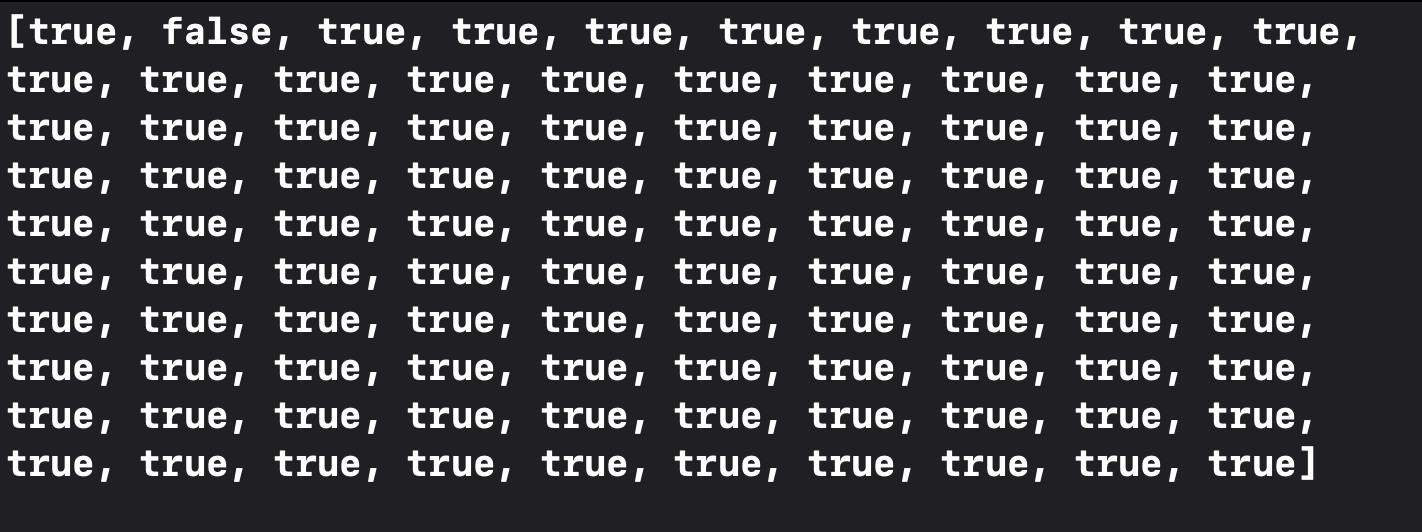
겉으로 보면 true가 마지막에 하나만 줄어든 거 말고는 다른 게.. 없음
근데 배열은 0부터 시작이 됨!!
100개를 생성하면 0~ 99까지만 만들어지고 있는 거임!!! 그래서 101개를 만들어줘야지 0~100까지 만들어져
1~ 100 사이의 소수를 구할 수 있음!!!
근데 사실 소수가 될 수 없는 1을
isPrimeNumber[0] = false
0번째부터 1번이라고 생각하면 사실문제는 없어 보이는데 배열 1번을 1부터 제거했다고 생각하는 게 좋아서 ~ 이렇게 하지 않았나라고 ~ 생각했음... 의도랑 다를 수 있음...

1을 제거한 모습이고

계속해서 소수가 될 수 없는 수들을 지워줌
2를 제외하고 2의 배수들을 지워주고
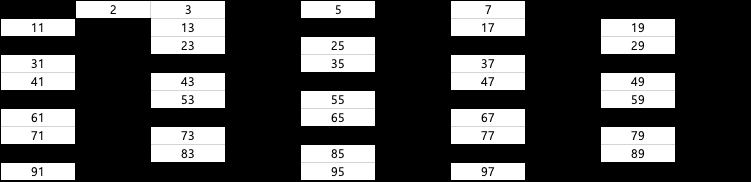
3을 제외하고 3의 배수들을 지워줌
다음은 4의 배수를 지워줘야햐지만 4는 2의 배수로써 이미 다 지워짐
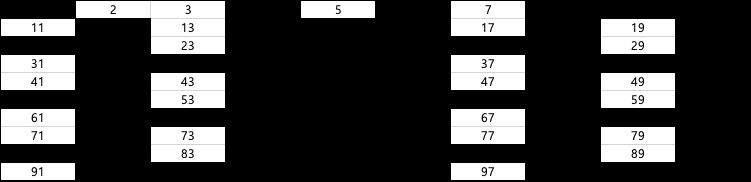
다시 5를 제외한 5의 배수들을 지워줌
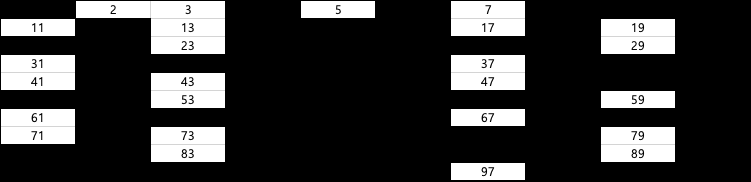
6은 이미 지워짐!! 7을 제외하고 7의 배수들을 지워줌
계속 지우는 걸 언제까지?? 해야 함??이라 생각할 때가 되었는데
100까지 해야 하는 거야???라고 하면 그렇지 않음!!
자! 예를 들어 77이란 수를 보자 ~ 77은 7 * 11 임
7을 제외한 7의 배수를 지워줄 때 이미 77은 지워졌음
그럼 11의 배수들은 11 배수를 지우기 전에 전부 지워짐!!!
22, 33, 44, 55, 66, 77, 88, 99 모두 지워졌음
그 말은 11은 고려 안 해줘도 된다는 말임
어떤 말이냐면 N 보다 작은 어떤 수 M이 있다고 했을 때
M 이 M = A*B 일 때 A와 B 둘 중 하나는 무조건 $$\sqrt {N}$$ 이하임
예를 들어보면 10 * 11 = 110이므로 100을 넘기기 때문에 안됨
근데 50 * 2 = 100 일 때는 둘 중 하나가 50으로 $$\sqrt {N}$$ 이상이 더라도 작은 수 2를 제외한 2의 배수를 제거할 때 이미 제거가 됨.
즉, $$\sqrt {N}$$ 보다 작은 수의 배수만 체크해도 전부 지워지기 때문에 $$\sqrt {N}$$ 까지 반복하면 됨!!!!.
2, 3, 5.. 의 배수를 지우는 것을 Swift 코드로 작성해 보면 ~
import Foundation
var isPrimeNumber = [Bool](repeating: true, count: 101)
isPrimeNumber[1] = false
for i in 2..<Int(sqrt(Double(100))) {
if isPrimeNumber[i] {
var j = 2
while i * j <= 100 {
isPrimeNumber[i*j] = false
j += 1
}
}
}

요런 결과가 나오는데 이제 소수인 true 값만 뽑아서 print 해주면 됨
for i in 1...100 {
if isPrimeNumber[i] {
print(i, terminator: " ")
}
}
// 2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97
고차함수로는 아래와 같이 나타낼 수도 있다!!
print(isPrimeNumber.enumerated().filter { $0.element && $0.offset > 1}.map {$0.offset})
// [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97]
최근 코테문제를 풀면서 알고리즘을 이용한 풀이를 많이 접하게 됨.
소수 구하는 문제도 마찬가지였음.
문제를 풀어보니깐 알고리즘 공부가 왜 필요한지 알게 됨!!!
참고 및 인용
'Algorithm' 카테고리의 다른 글
| [Algorithm] Swift 백준 10773번 (3) | 2024.04.06 |
|---|---|
| [Algorithm] Swift 유클리드 호제법 (최대공약수), 그리고 최소공배수 (2) | 2024.03.29 |
| [Algorithm] Swift 백준 1676번 (2) | 2024.03.15 |
| [Algorithm] Swift 백준 1259번 (1) | 2024.03.09 |
| [Algorithm] Swift 백준 1181번 (0) | 2024.02.18 |



